Cell Behavior Video Classification Challenge, a benchmark for computer vision methods in time-lapse microscopy

The classification of microscopy videos capturing complex cellular behaviors is crucial for understanding and quantifying the dynamics of biological processes over time. However, it remains a frontier in computer vision, requiring approaches that effectively model the shape and motion of objects without rigid boundaries, extract hierarchical spatiotemporal features from entire image sequences rather than static frames, and account for multiple objects within the field of view. To this end, we organized the Cell Behavior Video Classification Challenge (CBVCC), benchmarking 35 methods based on three approaches: classification of tracking-derived features, end-to-end deep learning architectures to directly learn spatiotemporal features from the entire video sequence without explicit cell tracking, or ensembling tracking-derived with image-derived features. We discuss the results achieved by the participants and compare the potential and limitations of each approach, serving as a basis to foster the development of computer vision methods for studying cellular dynamics.

Multi-Preconditioned LBFGS for Training Finite-Basis PINNs

A multi-preconditioned LBFGS (MP-LBFGS) algorithm is introduced for training finite-basis physics-informed neural networks (FBPINNs). The algorithm is motivated by the nonlinear additive Schwarz method and exploits the domain-decomposition-inspired additive architecture of FBPINNs, in which local neural networks are defined on subdomains, thereby localizing the network representation. Parallel, subdomain-local quasi-Newton corrections are then constructed on the corresponding local parts of the architecture. A key feature is a novel nonlinear multi-preconditioning mechanism, in which subdomain corrections are optimally combined through the solution of a low-dimensional subspace minimization problem. Numerical experiments indicate that MP-LBFGS can improve convergence speed, as well as model accuracy over standard LBFGS while incurring lower communication overhead.

Layer-Parallel Training for Transformers

We present a new training methodology for transformers using a multilevel, layer-parallel approach. Through a neural ODE formulation of transformers, our application of a multilevel parallel-in-time algorithm for the forward and backpropagation phases of training achieves parallel acceleration over the layer dimension. This dramatically enhances parallel scalability as the network depth increases, which is particularly useful for increasingly large foundational models. However, achieving this introduces errors that cause systematic bias in the gradients, which in turn reduces convergence when closer to the minima. We develop an algorithm to detect this critical transition and either switch to serial training or systematically increase the accuracy of layer-parallel training. Results, including BERT, GPT2, ViT, and machine translation architectures, demonstrate parallel-acceleration as well as accuracy commensurate with serial pre-training while fine-tuning is unaffected.

Data-Parallel Neural Network Training via Nonlinearly Preconditioned Trust-Region Method

Parallel training methods are increasingly relevant in machine learning (ML) due to the continuing growth in model and dataset sizes. We propose a variant of the Additively Preconditioned Trust-Region Strategy (APTS) for training deep neural networks (DNNs). The proposed APTS method utilizes a data-parallel approach to construct a nonlinear preconditioner employed in the nonlinear optimization strategy. In contrast to the common employment of Stochastic Gradient Descent (SGD) and Adaptive Moment Estimation (Adam), which are both variants of gradient descent (GD) algorithms, the APTS method implicitly adjusts the step sizes in each iteration, thereby removing the need for costly hyperparameter tuning. We demonstrate the performance of the proposed APTS variant using the MNIST and CIFAR-10 datasets. The results obtained indicate that the APTS variant proposed here achieves comparable validation accuracy to SGD and Adam, all while allowing for parallel training and obviating the need for expensive hyperparameter tuning.

Parallel Trust-Region Approaches in Neural Network Training: Beyond Traditional Methods

We propose to train neural networks (NNs) using a novel variant of the ``Additively Preconditioned Trust-region Strategy'' (APTS). The proposed method is based on a parallelizable additive domain decomposition approach applied to the neural network's parameters. Built upon the TR framework, the APTS method ensures global convergence towards a minimizer. Moreover, it eliminates the need for computationally expensive hyper-parameter tuning, as the TR algorithm automatically determines the step size in each iteration. We demonstrate the capabilities, strengths, and limitations of the proposed APTS training method by performing a series of numerical experiments. The presented numerical study includes a comparison with widely used training methods such as SGD, Adam, LBFGS, and the standard TR method.

Shape of my heart: Cardiac models through learned signed distance functions

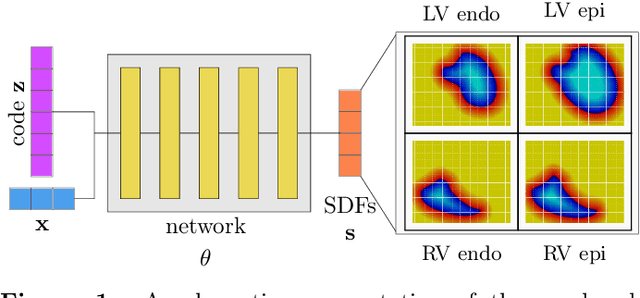
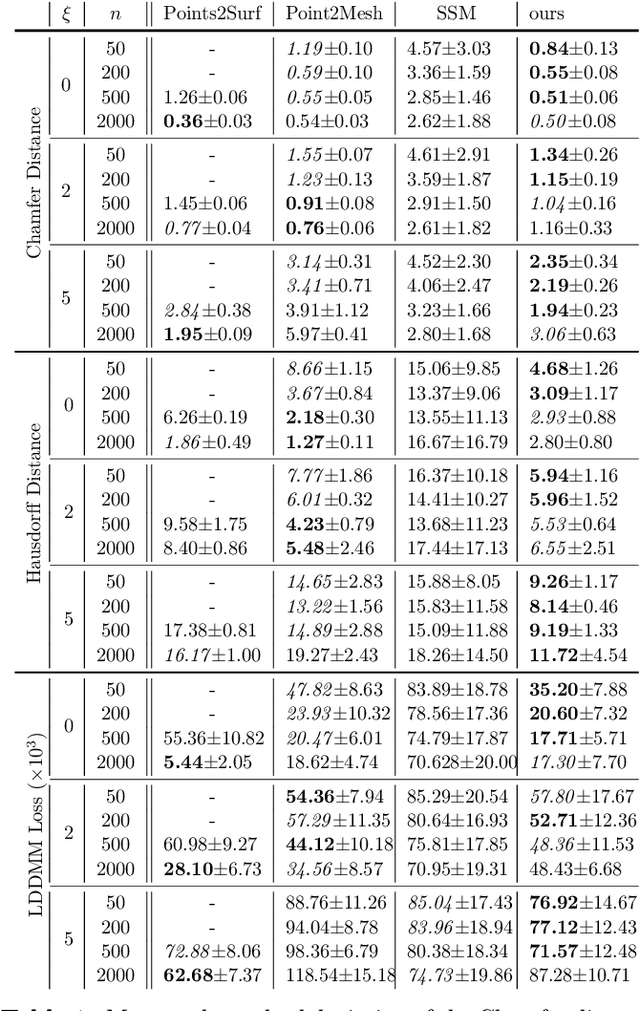
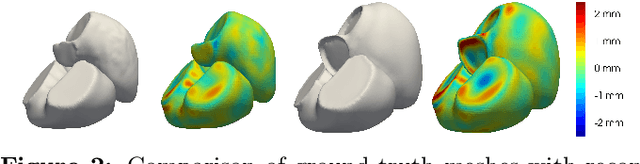
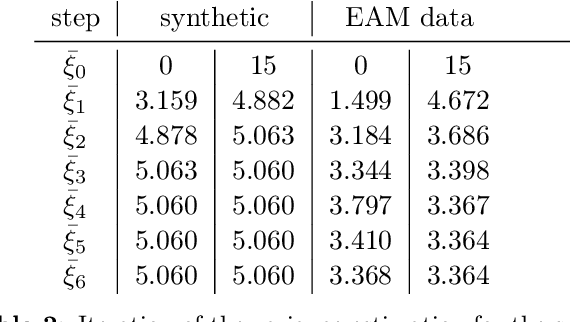
The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.

Enhancing training of physics-informed neural networks using domain-decomposition based preconditioning strategies

We propose to enhance the training of physics-informed neural networks (PINNs). To this aim, we introduce nonlinear additive and multiplicative preconditioning strategies for the widely used L-BFGS optimizer. The nonlinear preconditioners are constructed by utilizing the Schwarz domain-decomposition framework, where the parameters of the network are decomposed in a layer-wise manner. Through a series of numerical experiments, we demonstrate that both, additive and multiplicative preconditioners significantly improve the convergence of the standard L-BFGS optimizer, while providing more accurate solutions of the underlying partial differential equations. Moreover, the additive preconditioner is inherently parallel, thus giving rise to a novel approach to model parallelism.

Fast characterization of inducible regions of atrial fibrillation models with multi-fidelity Gaussian process classification

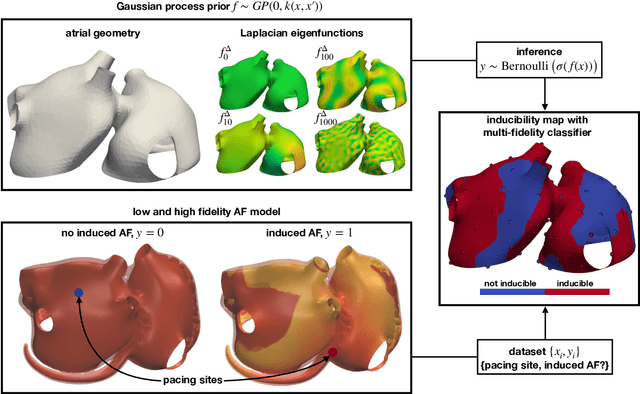
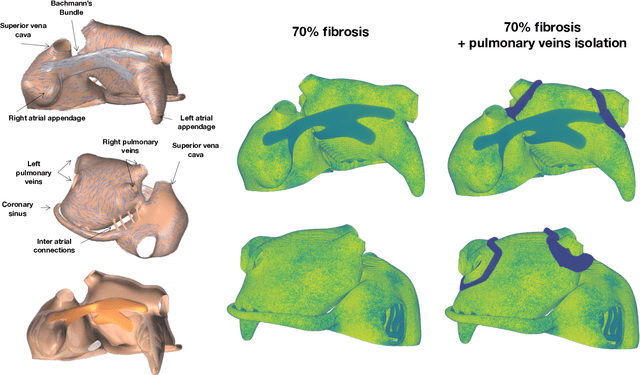
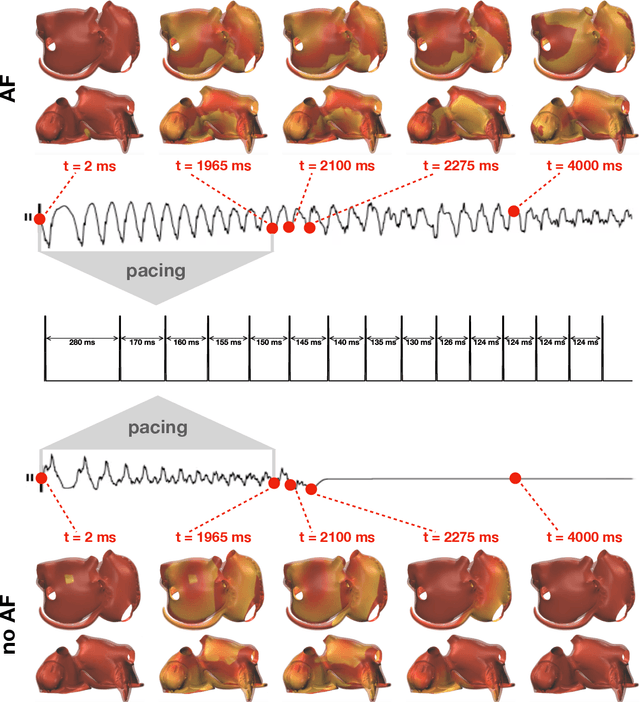
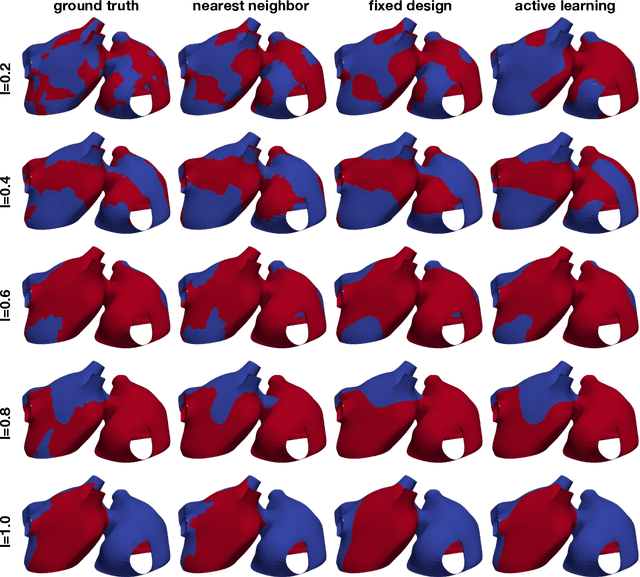
Computational models of atrial fibrillation have successfully been used to predict optimal ablation sites. A critical step to assess the effect of an ablation pattern is to pace the model from different, potentially random, locations to determine whether arrhythmias can be induced in the atria. In this work, we propose to use multi-fidelity Gaussian process classification on Riemannian manifolds to efficiently determine the regions in the atria where arrhythmias are inducible. We build a probabilistic classifier that operates directly on the atrial surface. We take advantage of lower resolution models to explore the atrial surface and combine seamlessly with high-resolution models to identify regions of inducibility. When trained with 40 samples, our multi-fidelity classifier shows a balanced accuracy that is 10% higher than a nearest neighbor classifier used as a baseline atrial fibrillation model, and 9% higher in presence of atrial fibrillation with ablations. We hope that this new technique will allow faster and more precise clinical applications of computational models for atrial fibrillation.

Construction of Grid Operators for Multilevel Solvers: a Neural Network Approach

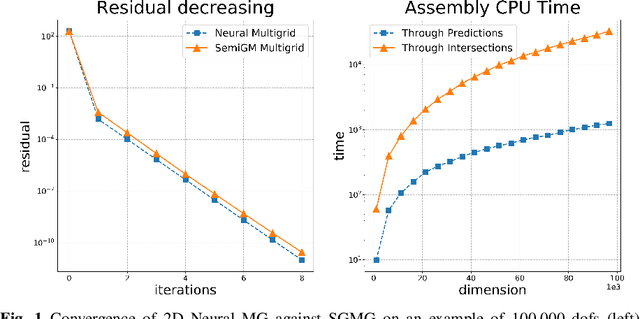
In this paper, we investigate the combination of multigrid methods and neural networks, starting from a Finite Element discretization of an elliptic PDE. Multigrid methods use interpolation operators to transfer information between different levels of approximation. These operators are crucial for fast convergence of multigrid, but they are generally unknown. We propose Deep Neural Network models for learning interpolation operators and we build a multilevel hierarchy based on the output of the network. We investigate the accuracy of the interpolation operator predicted by the Neural Network, testing it with different network architectures. This Neural Network approach for the construction of grid operators can then be extended for an automatic definition of multilevel solvers, allowing a portable solution in scientific computing

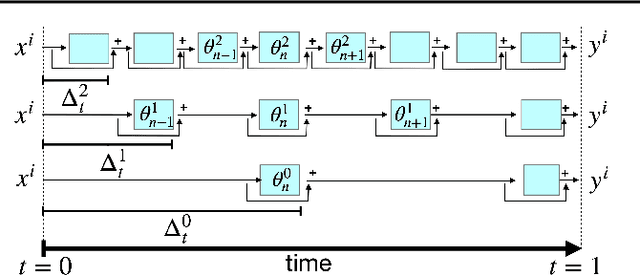
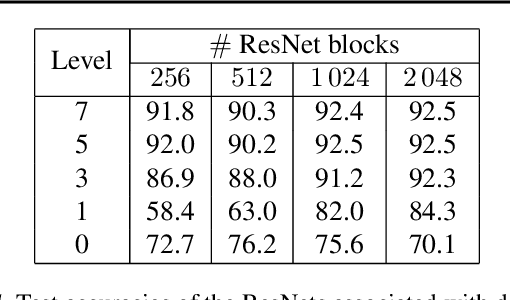
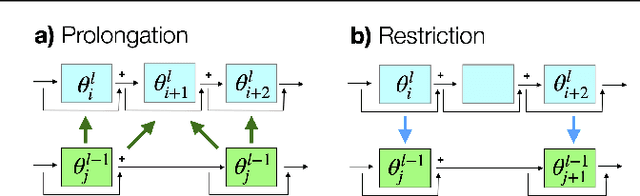
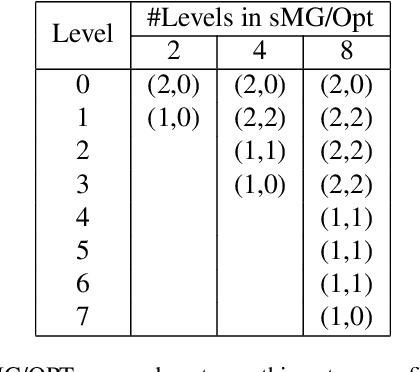
Training of deep residual networks with stochastic MG/OPT

We train deep residual networks with a stochastic variant of the nonlinear multigrid method MG/OPT. To build the multilevel hierarchy, we use the dynamical systems viewpoint specific to residual networks. We report significant speed-ups and additional robustness for training MNIST on deep residual networks. Our numerical experiments also indicate that multilevel training can be used as a pruning technique, as many of the auxiliary networks have accuracies comparable to the original network.